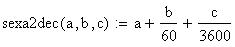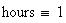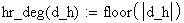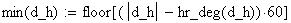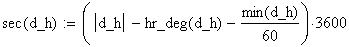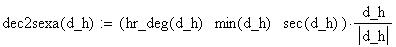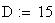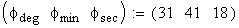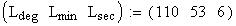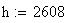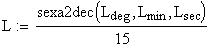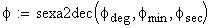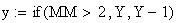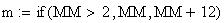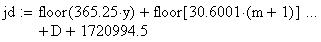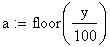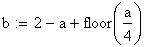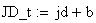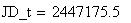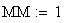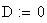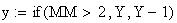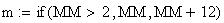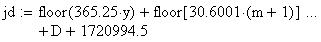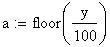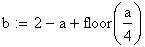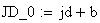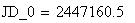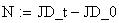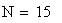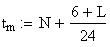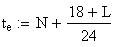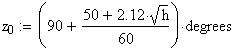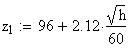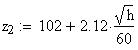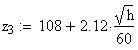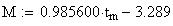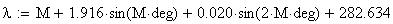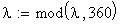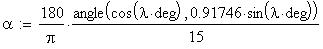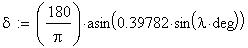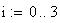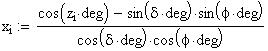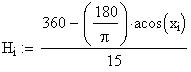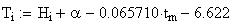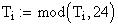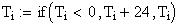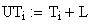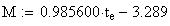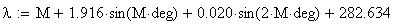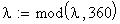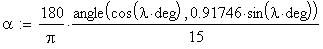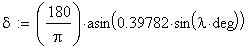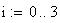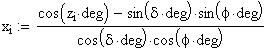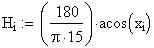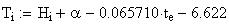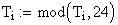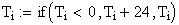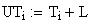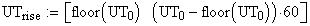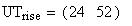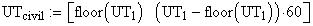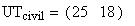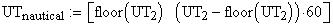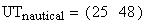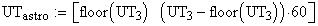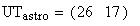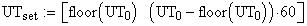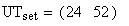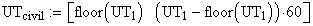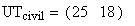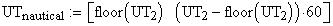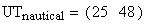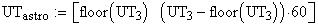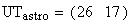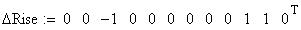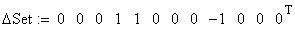The conversion function is given by

Reprinted from Astronomical Formulas by Martin Zombeck. Copyright (c) 1997 by MathSoft, Inc. All rights reserved.

where

a = integral number of degrees or hours

b = integral number of arc minutes or minutes of time

c = integral number of arc seconds or seconds of time

Introduction

This document calculates, for latitudes between 65 degrees North and 65 degrees South and any date in the latter half of the 20th century, the times of sunrise, sunset , and civil, nautical, and astronomical twilight . The calculated times refer to locations with a clear horizon and a standard refraction correction for normal meteorological conditions. The calculated times are accurate to within 2 minutes; higher accuracy is seldom justified since local meteorological conditions will cause the actual time to vary.

Unit Definitions:

Twilight is caused by the scattering of sunlight by the upper layers

of the Earth's atmosphere. There are different definitions of twilight.

Astronomical twilight begins at sunset (ends at sunrise) and ends (begins) when the Sun's center is 18 degrees below the horizon. Civil twilight begins (ends) when the Sun's center is 6 degrees below the horizon; nautical twilight begins (ends)

when the Sun's center is 12 degrees below the horizon.

Decimal (angles or time) to sexagesima l

We must first define some intermediate functions:

The method of the Almanac for Computers (United States Naval Observatory) is used to calculate the times.

The definitions for sunrise, sunset, and twilight for an observer at sea level are given in terms of the zenith distance z (p /2 - altitude) of the center of the Sun:

where d_h is the angle or time in decimal notation.

Sunrise and Sunset

90 deg 50 arc min

The conversion function is then given by

Civil Twilight

96

Nautical Twilight

102

Astronomical Twilight

108

Sunrise or Sunset is defined for a geocentric altitude of -50 arc minutes; 34 arc minutes is to correct for atmospheric refraction and 16 arc minutes is to correct for the Sun's semidiameter.

For an observer at a height h meters above sea level the following correction should be added to the zenith distances above:

2.12h1/2 arc minutes

The following formulae are used to compute the phenomena:

M = 0.985600t - 3.289 degrees

l = M + 1.916sin M + .020sin 2M + 282.634 degrees

tan a = 0.91746tan l

sin d = 0.39782sin l

x = cos H = (cos z - sin d sin f)/(cos d cos f)

T = H + a - 0.065710t - 6.622 hours

UT = T + L

where

• M = Sun's mean anomaly

• t = approximate time of phenomenon in days since 0 January, 0h UT

• l = Sun's true longitude

• a = Sun's right ascension

• d = Sun's declination

• H = Sun's local hour angle

• T = local mean time of phenomenon

• f = latitude of observer

• L = longitude of observer (east is negative; west is positive) in hours

• UT = Universal Time of phenomenon

Using the above formulae, the procedure from the Almanac for Computers is as follows:

1. Calculate an initial value for t from

t = N + (6h + L)/24

(for morning phenomenon)

t = N + (18h + L)/24

(for evening phenomenon)

where N is the day of the year.

2. Calculate M and l.

3. Solve for a, noting that a is in the same quadrant as L.

4. Solve for d.

5. Solve for H; the correct quadrant for H is given by the following rules:

rising phenomenon: H = 360 - arccos x

setting phenomenon: H = arccos x

6. Calculate T.

7. Calculate UT. To convert to the local time see the standard time conversions in Section 1.16.

Year:

Month:

Day of the Month:

Latitude:

Longitude:

Observer's height above horizon (meters):

Observer's location:

MMT Observatory, Arizona

Calculations

Convert to decimal form:

The functions necessary to convert between sexagesimal and decimal form are defined past the right margin of the page.

The day of the year N:

First, calculate the Julian Date for the calendar date at 0h UT:

Then calculate the Julian Date for the calendar date on 0 January, 0h UT for the given year:

Define an initial value for t, the approximate time of the phenomena:

(for morning phenomena)

(for evening phenomena)

The zenith distances for the phenomena:

for Sunrise or Sunset

for civil twilight

for nautical twilight

for astronomical twilight

Convert the time T to a range between 0 and 24h:

Calculate UT of the phenomenon. If UT is greater than 24h , the phenomenon occurs on the following day, Greenwich time. If UT is negative, the phenomenon occurs on the previous day, Greenwich time.

Convert the time T to a range between 0 and 24h:

Calculate UT of the phenomenon. If UT is greater than 24h , the phenomenon occurs on the following day, Greenwich time. If UT is negative, the phenomenon occurs on the previous day, Greenwich time.

Sunrise:

Civil twilight:

Nautical twilight:

Astronomical twilight:

Note: To convert to Eastern Standard Time (for example), subtract 5 hours from the above times.

Sunset:

Civil twilight:

Nautical twilight:

Astronomical twilight:

Note: To convert to Eastern Standard Time (for example), subtract 5 hours from the above times.

In order to provide the user with an indication of the accuracy of the above method, we have calculated the times of Sunrise and Sunset for the year 1993 and compared these times with those times provided by the Astronomical Almanac. The times were calculated for a latitude of 42 degrees and at the Greenwich meridian.

The differences in Sunrise DRise = Risealmanac - Risehandbook and Sunset D Set = Setalmanac - Sethandbook in minutes for the beginning of each of the twelve months of 1993 are:

A plot of the above differences: